For many years, we thought that the verification of arbitrary computations on Bitcoin was impossible due to the blockchain’s limited scripting capabilities.
This changed in October 2023 with the publication of the BitVM paper, which described a way to achieve optimistic validation of complex computations on Bitcoin. This is significant because it opens the door to endless possibilities, including the implementation of more decentralized bridges between Bitcoin and other networks. BitVM received the attention it deserved and it unlocked several new ideas and proposals by just showing that the impossible was actually possible without changes to the Bitcoin consensus.
In this article, we provide an overview of some of the existing proposals (at the time of writing) in order to help people keep track of this fast-evolving new area that we call the “disputable computation paradigm”.
The disputable computation paradigm
TrueBit pioneered the idea of verifying arbitrary computations on a blockchain. The idea consists of
- executing a program off-chain,
- submitting the proof of the execution on-chain, and
- running an on-chain validation if someone challenges the proof.
This reduces the amount of computations executed on-chain to a fraction of the total, which enables the verification of arbitrarily complex computations.
The paradigm establishes a way to represent the state of a computer and defines a computational task as a sequence of steps that modify this state. The trace of a computation is thus a sequence of states.
In order to validate a computational task, a prover runs the task off-chain and submits the final state of the computer to the blockchain. If nobody challenges the result, the computation is accepted by the network. A verifier who disagrees with the submitted result can engage in a verification game with the prover to resolve the dispute. After the game, the prover is penalized if the final state submitted was erroneous.
The verification game consists of a challenge-response protocol where the prover reveals information that the verifier requests. The verifier wins if the prover stops responding at any point, and thus, the prover is forced to reveal the requested information. Using this system, the verifier requests the state of the computer at certain steps. Since the verifier disagrees with the final state submitted by the prover, there must be an invalid state transition at some point in the computational trace. The verifier uses an iterative search process to pinpoint this invalid state transition, and forces the prover to reveal its details. The state transition is then executed on-chain and compared against the data submitted by the prover. The prover is penalized if the state transition is invalid using the data provided.
BitVM
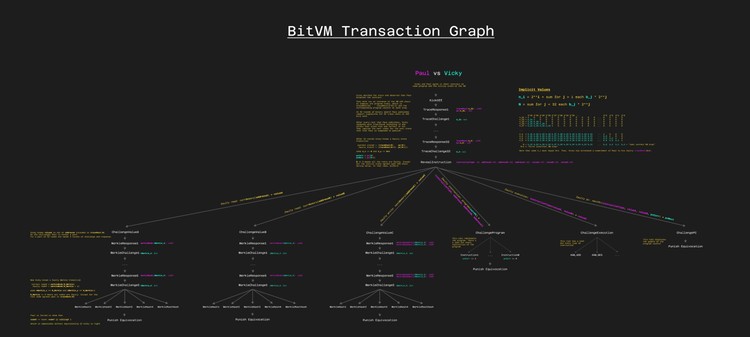
The original BitVM paper describes a way to build a verification game on Bitcoin where computations are expressed as a circuit of NAND gates. A more advanced design uses assembly-like instructions instead. This design represents the state of the computer at a certain step as the root of a Merkle tree where each leaf is a memory address and value. Each computational step reads two inputs from memory, executes an opcode, writes an output to memory, and modifies a program counter. The trace of the computation is the sequence of Merkle roots representing all the values in memory at each step.
BitVM organizes this trace in another Merkle tree where each leaf is the Merkle root of the memory at each computational step.
The verification game in BitVM starts with a binary search over the trace Merkle tree where the verifier identifies an invalid state transition. The prover submits the details of the conflicting computational step, including its inputs, opcode, and output. The verifier can then challenge different parts of the state transition, including the instruction type, the program counter, or the input or output values. Performing this binary search means that the verification game requires log2(n) rounds for n computational steps.
To guarantee the authenticity of all the data during the verification game the prover needs to sign all the information submitted on-chain using one-time Lamport signatures. The verifier instantly wins the verification game by showing equivocation, that is, two distinct messages signed with the same one-time public key belonging to the prover.
Verification game in BitVM
BitVM2
In BitVM, the verification game consists of a set of pre-signed transactions between the prover and the verifier. This can work with multiple verifiers under a 1-of-n honest assumption, but the set of verifiers needs to be defined during setup. BitVM2 is a replacement for BitVM that allows a multi-party setting where anyone can take the role of the verifier.
BitVM2 represents a computational task as a function f(x) = y where x is the input and y is the result. The task can be split into subtasks f1,f2,…, fn where f1(x) = z1, f2(z1) = z2, … , fn = y. If f(x) is a succinct zero-knowledge verifier, BitVM2 can validate any computation that can be expressed as a zero-knowledge proof.
The verification game in BitVM2 consists of a single transaction where the prover submits x, y, and all the intermediate results z. This transaction allows anyone to show that the result of one of the subtasks does not correspond with the intermediate result submitted by the prover. In this way, anyone can become the verifier by forcing the on-chain execution of the challenged subtask.
In BitVM2, there is a trade-off between the amount of data submitted and the amount of computation executed on-chain. The greater the number of subtasks, the greater the amount of intermediate results that need to be submitted but the lower the amount of computation that is executed on-chain. BitVM2 reduces the verification game to one round but significantly increases the amount of data submitted in a single transaction since the number of intermediate results required could be up to 1,000.
BitVMX
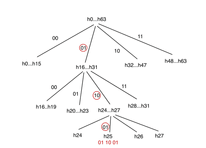
BitVMX is similar to BitVM in that it represents computations using assembly-like instructions. However, BitVMX does not use Merkle trees to organize the sequence of states. Instead, BitVMX creates a chain of hashes to represent the computer trace. This reduces the number of rounds required to identify the invalid state transition by enabling an m-ary search process that takes logm(n) rounds for n steps, where (m-1) is the number of states that the prover submits in each round. This allows for greater flexibility in the verification game and creates a trade-off between the amount of data submitted and the number of rounds required. In addition to this, BitVMX requires less storage than BitVM because it does not need to organize all memory positions in a Merkle tree. The verification game in BitVMX does not require a mechanism to punish equivocation like BitVM but requires two m-ary searches in the worst case, which translates into 2*logm(n) rounds where m could go from 2 up to 16.
n-ary search mechanism with 64 hashes (m = 64, n = 4, l = 3).
BitSNARK
BitSNARK represents computational tasks using only three types of instructions that operate with 256-bit registers. These three instruction types are enough to build a SNARK verifier, and thus, BitSNARK is limited to the verification of SNARK proofs. BitSNARK does not use addressable memory and defines the computer state at a particular step as the values in the 256-bit registers.
The verification game in BitSNARK consists of a binary search over the execution trace where, at each round, the prover submits the intermediate state of the registers at a particular step. After log2(n) rounds, the verifier is able to identify an invalid operation that is then executed on-chain for validation. The amount of data that the prover submits on-chain depends on the number of registers used to represent the state, which is expected to be less than 30. Apart from this, BitSNARK implements a mechanism to punish equivocation like BitVM.
SNARKnado
SNARKnado is another proposal that focuses on building a SNARK verifier instead of verifying arbitrary computations. SNARKnado represents computations as polynomial relations and runs the verification game directly on these polynomials. Given a polynomial, the verifier requests the prover to submit its evaluation at a random point. If the evaluation is incorrect, the search continues by splitting the polynomial into odd and even sub-polynomials. After a number of rounds, the verifier is able to identify the error in the computation. The number of rounds required is logarithmic in the degree of the polynomial and is estimated to be around 4. In this way, SNARKnado limits the number of rounds required in the verification game while keeping the amount of data submitted per round low.
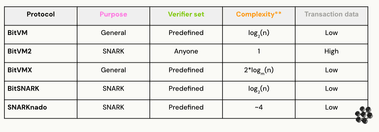
The following table shows a summary of the differences between the current existing protocols:
** m = [2, 4, …, 16] for BitVMX
Conclusion
The disputable computation paradigm on Bitcoin is evolving at a fast pace with the appearance of several proposals since the publication of the original BitVM paper. Most of the current efforts seem to be focused on SNARK verification and, with the discontinuation of BitVM in favor of BitVM2, BitVMX remains as the only solution designed as a general-purpose computer.
BitVM2 is the only protocol that requires just one round and that allows anyone to become the verifier, while the rest of the proposals define the set of verifiers during setup. BitVM2 achieves this at the cost of publishing more data in a single transaction. The other two SNARK-based protocols provide different trade-offs, with SNARKnado presumably achieving a better balance between the number of rounds and the amount of data submitted on-chain. Nevertheless, all solutions except for BitVM are still in development and their actual performance might depend on implementation details, as well as on specific use cases. In addition to this, we are likely to see protocol improvements and new proposals emerging in the coming months.