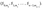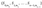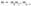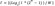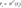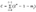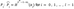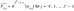Exploring Lamport and Winternitz Signatures for Stateful Bitcoin Scripts

BitVM is a framework designed to bring optimistic verification of any off-chain computation to the Bitcoin network, allowing for more complex operations such as zk rollups and sidechain bridges. BitVM enhances the flexibility of Bitcoin by introducing mechanisms to optimistically verify. BitVMX makes this even better by making sure operations are checked quickly and efficiently using different techniques. In this context optimistic verification This approach assumes that operations are valid until proven otherwise.

To keep these systems secure, BitVM and BitVMX use Lamport and Winternitz signatures. These cryptographic methods are key to making sure that the whole process has statefulness. By using these signatures, BitVM and BitVMX provide strong security that helps protect against different types of attacks and ensures that all operations work correctly.

This article will look into what Lamport and Winternitz signatures are, how the latter extends the former, and how they are used in BitVM. We will also explain how these signatures enable statefulness in BitVM and BitVMX, ensuring that certain variables that have been set previously can not be modified and reused in later scripts. 

First time hearing about BitVMX? Read the simplified BitVMX whitepaper here.

Understanding Lamport and Winternitz Signatures

A digital signature is a mathematical scheme for verifying the authenticity and integrity of digital messages or documents. In a nutshell:

• Lamport signatures employ one-time digital commitments, typically based on hash functions, to provide unforgeable signatures.
• Winternitz signatures utilize iterative applications of a one-way function, often in a chain, to achieve cryptographic security.

Lamport Signatures:  Devised by Leslie Lamport in the late 1970s, Lamport signatures are a type of hash-based digital signature scheme. They derive their security from the one-way nature of cryptographic hash functions. Lamport signatures are renowned for their simplicity and resistance against quantum computing attacks. They operate by pre-generating a large number of key pairs and using them to sign messages. However, their large signature size can be a limitation in some applications.

Winternitz Signatures: Proposed by Ralph Merkle and independently by Robert Winternitz, Winternitz signatures are another variant of hash-based digital signatures. They offer similar security properties to Lamport signatures but with improved efficiency. Winternitz signatures employ a chain structure to reduce the size of the signature compared to Lamport, making them more practical for real-world applications. By allowing the user to adjust the Winternitz parameter, these signatures enable a balance between computational speed and signature size, effectively generalizing the Lamport scheme.

Lamport: a formal view

In this section, we provide a detailed, step-by-step explanation of how Lamport signatures are generated, used, and verified. We explore the technical aspects of the key generation process, message signing, and signature verification. Finally, we discuss the security considerations and vulnerabilities associated with it.

Key Generation

Generate two random strings (bit sequences) Sᵢ,₀ and  Sᵢ,₁ for each bit i in the message, where i ranges from 0 to 𝑛−1 for an n-bit message.

The private key consists of the pairs (Sᵢ,₀,Sᵢ,₁) for 𝑖=0,1,…,𝑛−1.

For each pair (Sᵢ,₀,Sᵢ,₁) in the private key, compute their hash values (H(Sᵢ,₀),H(Sᵢ,₁)).

The public key consists of these hash pairs (H(Sᵢ,₀),H(Sᵢ,₁)) for 𝑖=0,1,…,𝑛−1.

Signing a Message

Convert the message m to be signed into its binary form m= m₀m₁…m-1, where each mi is a bit (0 or 1).

For each bit mi of the message, include the corresponding Sᵢ,mᵢ from the private key in the signature.

The signature is a sequence of n elements:

Verifying a Signature

Given a message m its signature

Convert the message m into its binary form

For each bit mᵢ, compute the hash of the corresponding part of the signature: H(Sᵢ,ₘᵢ).

Verify that each computed hash H(Sᵢ,ₘᵢ) matches the corresponding part of the public key H(Sᵢ,₀) or H(Sᵢ,₁).

Security Considerations

• One-Time Use: Lamport signatures are secure only if each key pair is used to sign one message. Using the same key pair to sign multiple messages reveals parts of the private key, compromising the security.
• Hash Function: The security of Lamport signatures relies on the strength of the cryptographic hash function used. It should be resistant to preimage attacks, second-preimage attacks, and collision attacks.

Why Are They Called One-Time Signatures?

Lamport signatures are referred to as one-time signatures because their security significantly degrades when the same key is used to sign more than one message. The core reason for this is that each additional signature reveals more information about the private key, making it easier for an attacker to forge a signature. 

When a single signature is observed, an attacker learns one hash from each pair in the key. However, with two signatures, the attacker knows both hashes from half of the pairs and one hash from the other half. With three signatures, the attacker knows both hashes from three-quarters of the pairs and so on. This progressive disclosure means that the security level effectively halves with each additional signature. 

For instance, if a key is designed to offer 256-bit security against second-preimage attacks and 128-bit security against collision attacks, practical attacks become possible after the same key is used three times. By the fourth use, it becomes trivial to find message-signature pairs. This vulnerability arises because the attacker can use the known hashes to construct new valid signatures for messages of their choosing, particularly if the messages have some flexibility in their content.

Vulnerability of Lamport Signatures When Used More Than Once

The primary vulnerability of Lamport signatures when reused is that an attacker can forge signatures for arbitrary messages by leveraging the information gained from previously observed signatures. Suppose an attacker has access to signatures for multiple messages signed with the same key. In that case, they can construct a new valid signature by piecing together parts of the known signatures.

For example, consider the following scenario with 16-bit messages:

Signed messages: m₁= 0001111101110001 and  m₂= 0111110000111111. An attacker can forge a signature for a new message m* = 0101111000110101 by combining parts of the signatures for m₁ and m₂. This attack works because the attacker can choose the bits from m₁ and m₂ that match the corresponding bits in m*. The attacker only needs the hashes that correspond to the differing bits in m₁ and m₂ to construct the signature.

When messages are hashed before signing, the attack becomes more complex but remains feasible. The attacker must find a message m* whose hash shares enough bits with the hashes of the previously signed messages. Each additional signature observed reduces the number of required hash evaluations, making forgery progressively easier.

In essence, Lamport signatures should only be used once per key to maintain their security. Reusing the same key for multiple messages allows attackers to gather sufficient information to forge new signatures, compromising the integrity of the cryptographic system.

Winternitz from a theoretical perspective

As we already introduced, Winternitz’s one-time signature scheme (WOTS) is an enhancement of Lamport signatures that dramatically shrinks the signature and public-key size. But there is no such thing as a free lunch. This improvement comes at the cost of more work to generate and verify signatures. In the following, we provide a formal definition and explanation of how Winternitz signatures work:

Parameters and Setup

• W: The Winternitz parameter, a positive integer that determines the number of bits processed at a time.
• n: Length of the hash output in bits.
• l: Number of segments in the message digest, calculated as l= ⌈n/W⌉. Where ⌈ ⌉means the smallest integer greater than or equal to a given number.
• l’: Checksum length, calculated as
• L: Total length of the signature, L=l+l’ .

Key Generation

Generate L random bit strings Sᵢ of length n for i= 0 , 1 , … , L-1.

The private key consists of these random bit strings S=(S₀ , S₁ , … , Sₗ₋₁).

For each private key segment  Sᵢ,  apply the hash function iteratively 2ʷ times: .

The public key is the sequence of these hash results P= (P₀ , P₁ , … , Pₗ₋₁).

Signing a Message

Split the message m into l segments of W bits each: m= (m₀ , m₁ , … , mₗ₋₁ ).

Calculate the checksum C as

Convert the checksum C into l’ segments of W bits each: C=(c₀ , c₁ , … , cₗ’₋₁).
Generally, the CheckSum will be a single segment: C=(c₀ ).

For each segment mᵢ of the digest and checksum cᵢ, derive the signature δᵢ by hashing the corresponding private key segment mᵢ times: for i= 0 , 1 , … , l-1.

Similarly, for the checksum segments:  for  j= 0 , 1 , … ,l’-1.

The complete signature is the concatenation of these segments: =(0 ,1 , … , L-1).

Verifying a Signature

Given the message m and its signature δ =(δ₀ ,δ₁ , … ,δₗ₋₁).

Split the message m into l segments: m= (m₀ , m₁ , … , mₗ₋₁)

Calculate the checksum C  and split it into l’ segments: C=(c₀ , c₁ , … , cₗ’₋₁ ).

For each signature segment δᵢ, apply the hash function 2ʷ-1-mᵢ times to derive the expected public key segment

Similarly, for the checksum segments:

The signature is valid if the derived public key  matches the original public key (P₀ , P₁ , … , P₋₁).

Security Considerations

• Parameter Selection: The choice of W affects the trade-off between signature size and computational efficiency. Larger W values reduce the signature size but increase the computational effort for both signing and verification.
• One-Time Use: Like Lamport signatures, Winternitz signatures are also one-time use. Reusing the same key pair for multiple messages compromises security by revealing information about the private key.

The following diagram shows the sequence of Winternitz chains for each segment that the message that has been split. Each arrow represents an evaluation in a hash function.

Why the Checksum is Necessary

The checksum in the Winternitz signature scheme is essential for maintaining security and ensuring the integrity of the signature process from a technical standpoint.

The Winternitz signature scheme involves dividing the message into segments and hashing each segment multiple times. When a signature is created, each segment of the message digest is hashed a specific number of times based on its value. However, this process introduces a vulnerability: if an attacker knows the value of any segment, they can construct valid signatures for any subsequent elements in the hash chain. This is because revealing a member of the hash sequence allows the attacker to compute all subsequent hashes, compromising the integrity of the signature.

To eliminate this risk, the checksum is key.. It ensures that any alteration in the message would require a corresponding and consistent alteration in the checksum, which is computationally infeasible without the private key. Because using a later hash in the value needs a previous value on the checksum (that is indeed infeasible without the private key). The checksum acts as an additional layer of verification, making it impossible without a preimage attack for an attacker to create a valid signature without access to the private key.

Additionally, the checksum ensures the completeness of the signature process. It acts as a final check, verifying that no bits are lost or altered during signing. This guarantees that the entire message is accounted for and correctly represented in the signature.

Furthermore, the checksum balances the hash iterations for all segments, validating the overall integrity of the signature. This means that the correct number of hash iterations is applied, ensuring that the signature is both accurate and secure.

Without the checksum, the scheme becomes vulnerable to attacks. An attacker could more easily alter message segments and create valid signatures without the private key. The absence of a checksum could also lead to incomplete verification, allowing altered or partial messages to be accepted as authentic.

BitVM and BitVMX: Where Lamport and Winternitz Signatures Shine

As we have already mentioned BitVM and BitVMX are frameworks designed to bring optimistic verification of any off-chain computation to the Bitcoin network. Both can employ either Lamport or Winternitz signatures to create robust data commitments. In this context, a commitment is a cryptographic assurance that certain data exists, has been securely recorded at a specific point in time, and signed. These commitments can then be referenced in future challenges by another party. The use of these signatures ensures that each commitment is both verifiable and tamper-proof.

If the verifier(s) agree with the operator, there is nothing more to be done, and the operations proceed as usual. However, if the verifier disagrees with the operator, since both have publicly signed these commitments, the protocol allows both of them to use the other one’s information to demonstrate they are trying to cheat or are making an erroneous operation.

One of the key innovations introduced by BitVM is the ability to maintain and reference the state across multiple transactions. This is achieved by using one-time signatures to commit to the state at each step. By leveraging Lamport and Winternitz signatures, BitVM ensures that each state transition is securely committed and can be referenced reliably in subsequent operations. Winternitz signatures facilitate efficient commitments. Their structure allows for quick verification, which is crucial for maintaining the performance of the Bitcoin network.

Advantages of Lamport and Winternitz Signatures in BitVM and BitVMX

• Verification Speed: Winternitz signatures are designed for rapid verification, which is essential for maintaining the efficiency of the Bitcoin network. Their use in transaction commitments and state updates ensures that these operations can be performed without compromising security.
• Reduced Overhead: Compared to other signature schemes, Winternitz signatures generate smaller signature sizes, which reduces the overall transaction size.
• Quantum Resistance: Both Lamport and Winternitz signatures offer strong resistance against quantum computing attacks. This is a critical advantage against the potential threat posed by quantum computers.
• Tamper-Proof Commitments: The use of these signatures ensures that once a commitment is made, it cannot be altered without detection. This tamper-proof nature is vital for maintaining the integrity of stateful smart contracts and ensuring that all participants can trust the recorded data.
• Stateful: The primary use case for these signatures in BitVM and BitVMX is to enable stateful smart contracts. By allowing commitments made in one transaction to be referenced in future transactions, they provide a mechanism for maintaining and managing state across multiple interactions. This capability is essential for implementing more sophisticated logic on the Bitcoin network

Conclusion

In conclusion, Lamport and Winternitz signatures have a great number of properties that make them suitable for use in BitVM and BitVMX. Their integration into those protocols significantly enhances Bitcoin’s scripting capabilities by enabling efficient and secure stateful operations. Their use in data commitments ensures that the network can handle more complex transactions while maintaining high levels of security and performance. These cryptographic techniques are key to the future of Bitcoin as they pave the way for more advanced and secure decentralized applications such as trust-minimized sidechain bridges, optimistically verifying zero-knowledge proofs on Bitcoin.